|
How are
bits distributed between each of the real number components ??
 That
is a tough question. First, we need to know how many total bits are involved.
Remember:
THIS IS A
ZERO-SUM SITUATION!
We know that 1-bit will be
allocated to the sign. However the remaining bits must be split between the
mantissa and the characteristic of the exponent. For every bit allocated to the
mantissa, there is 1-bit less for the characteristic of the exponent.
Let's assume that we
decide to store the real number on 16-bits (the same as a short integer). Since
we know that 1-bit will be used for the sign-bit, that leaves 15-bits to
distribute between the mantissa and the characteristic of the exponent. Let's
look at all the possible distributions and what the distributions for each
component:
|
Mantissa Bits |
Mantissa Range |
Precision (digits) |
Characteristic Bits |
Characteristic Range |
|
1 |
0 ... 21
- 1 => 0 ..1 |
0 |
14 |
-213 to 213
- 1 => -8, 192 to +8,191 |
|
2 |
0 ... 22
- 1 => 0 ..3 |
0 |
13 |
-212 to 212
- 1 => -4, 096 to +4,095 |
|
3 |
0 ... 23
- 1 => 0 ..7 |
0 |
12 |
-211 to 211
- 1 => -2, 048 to +2,047 |
|
4 |
0 ... 24
- 1 => 0 ..15 |
1 |
11 |
-210 to 210
- 1 => -1, 024 to +1,024 |
|
5 |
0 ... 25
- 1 => 0 ..31 |
1 |
10 |
-29 to 29
- 1 => -512 to +511 |
|
6 |
0 ... 26
- 1 => 0 ..63 |
1 |
9 |
-28 to 28
- 1 => -256 to +255 |
|
7 |
0 ... 27
- 1 => 0 ..127 |
2 |
8 |
-27 to 27
- 1 => -128 to +127 |
|
8 |
0 ... 28
- 1 => 0 ..255 |
2 |
7 |
-26 to 26
- 1 => -64 to +63 |
|
9 |
0 ... 29
- 1 => 0 ..511 |
2 |
6 |
-25 to 25
- 1 => -32 to +31 |
|
10 |
0 ... 210
- 1 => 0 ..1023 |
3 |
5 |
-24 to 24
- 1 => -16 to +15 |
|
11 |
0 ... 211
- 1 => 0 ..2047 |
3 |
4 |
-23 to 23
- 1 => -8 to +7 |
|
12 |
0 ... 212
- 1 => 0 ..4095 |
3 |
3 |
-22 to 22
- 1 => -4 to +3 |
|
13 |
0 ... 213
- 1 => 0 ..8191 |
3 |
2 |
-21 to 21
- 1 => -2 to +1 |
|
14 |
0
... 214 - 1 => 0 ..16383 |
4 |
1 |
-20 to 20
- 1 => -1 to +0 |
Which is the best bit distribution
??
Basically, each of the
above combinations are terrible. Our level of precision is inadequate, and
while we may get an adequate characteristic of exponent range, the
corresponding mantissa range (precision level) is horrible.
What can we do ??
The same thing we've
always done in this situation: ADD MORE BITS!
How many??
Let's double the number
of bits: 32. Once again, we know that 1-bit will be used for the
sign-bit, that leaves 31-bits to distribute between the mantissa and the
characteristic of the exponent. Let's look at some of the possible
distributions and what the distributions for each component:
|
Mantissa Bits |
Mantissa Range |
Precision (digits) |
Characteristic Bits |
Characteristic Range |
|
15 |
0
... 215 - 1 => 0 ..
32,767 |
4 |
16 |
-215 to 215
- 1 => -32,768 to +32,767 |
|
16 |
0
... 216 - 1 => 0 ..
65,535 |
4 |
15 |
-214 to 214
- 1 => -16,384 to +16,383 |
|
17 |
0
... 217 - 1 => 0 .. 131,071 |
5 |
14 |
-213 to 213
- 1 => -8,192 to +8,191 |
|
18 |
0
... 218 - 1 => 0 .. 262,143 |
5 |
13 |
-212 to 212
- 1 => -4, 096 to +4,095 |
|
19 |
0
... 219 - 1 => 0 ..
524,288 |
5 |
12 |
-211 to 211
- 1 => -2, 048 to +2,047 |
|
20 |
0
... 220 - 1 => 0 .. 1,048,575 |
6 |
11 |
-210 to 210
- 1 => -1, 024 to +1,024 |
|
21 |
0
... 221 - 1 => 0 .. 2,097,151 |
6 |
10 |
-29 to 29
- 1 => -512 to +511 |
|
22 |
0
... 222 - 1 => 0 .. 4,194,303 |
6 |
9 |
-28 to 28
- 1 => -256 to +255 |
|
23 |
0
... 223 - 1 => 0 .. 8,388,607 |
6 |
8 |
-27 to 27
- 1 => -128 to +127 |
|
24 |
0
... 224 - 1 => 0 .. 16,777,215 |
7 |
7 |
-26 to 26
- 1 => -64 to +63 |
|
25 |
0
... 225 - 1 => 0 .. 33,554,431 |
7 |
6 |
-25 to 25
- 1 => -32 to +31 |
|
26 |
0
... 226 - 1 => 0 .. 67,108,864 |
7 |
5 |
-24 to 24
- 1 => -16 to +15 |
|
27 |
0
... 227 - 1 => 0 .. 134,217,727 |
8 |
4 |
-23 to 23
- 1 => -8 to +7 |
|
28 |
0
... 228 - 1 => 0 .. 268,435,457 |
8 |
3 |
-22 to 22
- 1 => -4 to +3 |
Which distribution is best ??
Still a tough question. It
does make sense to consider the distributions where the precision level changes:
|
Mantissa Bits |
Mantissa Range |
Precision (digits) |
Characteristic Bits |
Characteristic Range |
|
17 |
0
... 217 - 1 => 0 .. 131,071 |
5 |
14 |
-213 to 213
- 1 => -8,192 to +8,191 |
|
20 |
0
... 220 - 1 => 0 .. 1,048,575 |
6 |
11 |
-210 to 210
- 1 => -1, 024 to +1,024 |
|
24 |
0
... 224 - 1 => 0 .. 16,777,215 |
7 |
7 |
-26 to 26
- 1 => -64 to +63 |
|
27 |
0
... 227 - 1 => 0 .. 134,217,727 |
8 |
4 |
-23 to 23
- 1 => -8 to +7 |
So, which one ??
Although not quite
universal, the most common distribution is:
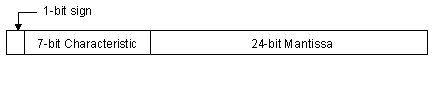
Note that this will allow for:
|
Mantissa Bits |
Mantissa Range |
Precision (digits) |
Characteristic Bits |
Characteristic Range |
|
24 |
0
... 224 - 1 => 0 .. 16,777,215 |
7 |
7 |
-26 to 26
- 1 => -64 to +63 |
How do we determine the range of
real numbers?
That is our next tutorial.
This page was last updated on
05/31/05
|
CIS3355:
Business Data Structures